復習と進度確認

[配布資料PDF版]

[テーマ] クロス表の整形と解釈の方法

前回課題について

2×3のクロス表なので、 m=2 である。このため、m-1=1 となるので、結局 V = √(χ² / ( N(m-1) ) ) = √( χ² / N ) である。PSPPの出力にあてはめて確認してみるとよい。

式 [4-17] のなかでは、

「Pearson のカイ2乗」 = 式全体の値
「観測度数」= 「セルの度数の実際の値」
「期待度数」= 「セルの度数の予測値」
「残差」= 分子の括弧の中
「標準残差」= 分数全体 (Σ の中身) の平方根

添字を使った表記 (たとえば n₁₁ や n_1. や n_.1 など) を覚えておくとよい。

連関係数 V は

独立 (無関連) のとき最小値0
関連が強くなるほど大きくなる
完全関連のとき最大値1をとる

「完全な」関連とは? → 教科書 p. 115

連関係数の解釈

連関係数は、「モデル」と「データ」の乖離を表した値と解釈できる

特定のモデル (この場合、独立の状態) の下で予測される値 (この場合、期待度数) を求める
実際のデータの値 (この場合、観測度数) と比較する
モデルから予測される値と実際のデータの値の違いを集計する
0～１の範囲の係数になるように調整する (→ ちがうデータ間で比較しやすくなる)

多くの統計手法で、このタイプの「○○係数」が使われる。

連関係数 V の大きさの評価は主観的な問題であり、対象とする変数の性質によって基準が変わる。非常に大雑把には、つぎのような値を目安にするとよい：

0.1 未満 …… 関連はない (無視してよい程度)
0.2 程度 …… 弱い関連
0.3 程度 …… そこそこの関連
それ以上 …… 強い関連

連関係数とφ係数、％との関連

PSPP では √(χ² / N) の値を Phi (ファイ = φ) として出力する。ただし、2×2クロス表のときは、これに符号をつけて関連の方向性を示す (マイナスになる場合がある)。 m=2 のときは、V = |φ| である。φ係数については (おなじ値に帰着する) 別の計算方法がある (教科書 p. 110)。

2×2クロス表においては、φ係数と％の差との間には、一定の関係がある。

教科書 pp. 112--114 の記述を読んで、どのような関係があるか理解する
実際のデータで2×2クロス表を出力して、確認してみよう

論文等のための表の書きかた

自分だけが見て参考にする場合はどういう表の書きかたでもよいが、人に見せる表については、きちんと整形する。

カテゴリーの並べ順や行列の組み合わせをわかりやすく
変数とカテゴリーの命名
表のタイトルとして適切なものをつける

タイトル、表本体、注釈を読めばそれだけでわかるように書くこと。縦罫線はなるべく引かない。文字列は左揃え、数字は小数点揃えが基本。

表の実例：

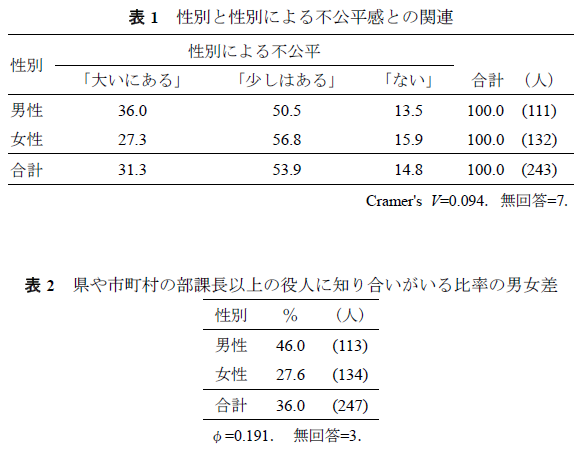
表に書くべき要素はつぎのとおり：

各セルの行 (または列) ％
行 (または列) 合計の度数と「100.0%」
列 (または行) 合計の％
全体の度数
連関係数Cramer の V (またはφ)
欠損数とその原因

行→列の因果を想定して表を書くのがふつうだが、ページ中の配置などの都合によっては列→行でもよい。方向は、合計の「100.0」で区別する。

全度数が1000人以下であれば、％は小数第1位まででよい。
Vやφなどの係数は小数第3位まで

2列表の場合は、1列の％だけ示してもよい

復習事項

PSPPの操作

データエディタにおける「変数ビュー」の使いかた
「欠損値」(missing value) とは何か
シンタックス (syntax) とは何か
変数値の再割り当ての方法
グループに分割する方法
度数分布表における「パーセント」と「有効パーセント」のちがい
度数分布表における「累積パーセント」の利用法
グラフの作成
「出力ビューア」の扱い

統計分析の基礎など

尺度水準とは何か。それはなぜ重要か。
Excel によるグラフの書きかた

クロス表

「行」「列」「セル」「周辺度数」
「行％」と「列％」の使い分け
クロス表をグラフにするときは、どのような種類のグラフが適切か

この授業のインデックス

前回の授業 | 次回の授業

TANAKA Sigeto

History of this page:

2020-06-05 : Created
2020-06-05 : Minor corrections

This page is monolingual in Japanese (encoded in accordance with MS-Kanji: "Shift JIS").

Generated 2020-06-05 21:11 +0900 with Plain2.